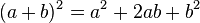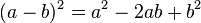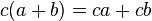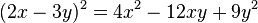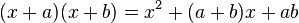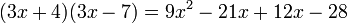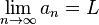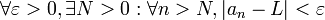GLOSARIO:

DERIVA:
 En matemáticas, la derivada de una función es una medida de la rapidez con la que cambia el valor de dicha función según cambie el valor de su variable independiente. La derivada de una función es un concepto local, es decir, se calcula como el límite de la rapidez de cambio media de la función en un cierto intervalo, cuando el intervalo considerado para la variable independiente se toma cada vez más pequeño. Por ello se habla del valor de la derivada de una cierta función en un punto dado.


Un ejemplo habitual aparece al estudiar el movimiento: si una función representa la posición de un objeto con respecto al tiempo, su derivada es la velocidad de dicho objeto. Un avión que realice un vuelo transatlántico de 4500 km en entre las 12:00 y las 18:00, viaja a una velocidad media de 750 km/h. Sin embargo, puede estar viajando a velocidades mayores o menores en distintos tramos de la ruta. En particular, si entre las 15:00 y las 15:30 recorre 400 km, su velocida media en ese tramo es de 800 km/h. Para conocer su velocidad instantánea a las 15:20, por ejemplo, es necesario calcular la velocidad media en intervalos de tiempo cada vez menores alrededor de esta hora: entre las 15:15 y las 15:25, entre las 15:19 y las 15:21, etc.
El valor de la derivada de una función en un punto puede interpretase geométricamente, ya que se corresponde con pendiente de la recta tangente a la gráfica de la función en dicho punto. La recta tangente es a su vez la gráfica de la mejor aproximación lineal de la función alrededor de dicho punto. La noción de derivada puede generalizarse para el caso de funciones de más de una variable con la derivada parcial y el diferencial.
La derivada de una función f en un punto x se denota como f′(x). La función cuyo valor en cada punto x es esta derivada es la llamada función derivada de f, denotada por f′. El proceso de encontrar la derivada de una función se denomina diferenciación, y es una de las herramientas principales en el área de las matemáticas conocida como cálculo.

DIFERENCIAL:
Una ecuación diferencial es una ecuación en la que intervienen derivadas de una o más funciones desconocidas. Dependiendo del número de variables independientes respecto de las que se deriva, las ecuaciones diferenciales se dividen en:

• Ecuaciones diferenciales ordinarias: aquellas que contienen derivadas respecto a una sola variable independiente.
• Ecuaciones en derivadas parciales: aquellas que contienen derivadas respecto a dos o más variables.
• Una ecuación diferencial es una ecuación que incluye expresiones o términos que involucran a una función matemática incógnita y sus derivadas. Algunos ejemplos de ecuaciones diferenciales son:
  
  • 

  es una ecuación diferencial ordinaria, donde representa una función no especificada de la variable independiente 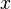, es decir, , es la derivada de con respecto a .

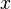  • La expresión

  es una ecuación en derivadas parciales.

  A la variable dependiente también se le llama función incógnita (desconocida). La resolución de ecuaciones diferenciales es un tipo de problema matemático que consiste en buscar una función que cumpla una determinada ecuación diferencial. Se puede llevar a cabo mediante un método específico para la ecuación diferencial en cuestión o mediante una transformada (como, por ejemplo, la transformada de La place).
  
  INTEGRAL INDEFINIDA: 
  Integral indefinida es el conjunto de las infinitas primitivas que puede tener una función.
  
  Se representa por ∫ f(x) dx.
  Se lee : integral de x diferencial de x.
  ∫ es el signo de integración.
  f(x) es el integrando o función a integrar.
  dx es diferencial de x, e indica cuál es la variable de la función que se integra.
  C es la constante de integración y puede tomar cualquier valor numérico real.
  Si F(x) es una primitiva de f(x) se tiene que:
  ∫ f(x) dx = F(x) + C
  Para comprobar que la primitiva de una función es correcta basta con derivar.

  Propiedades de la integral indefinida

  1. La integral de una suma de funciones es igual a la suma de las integrales de esas funciones.
  ∫[f(x) + g(x)] dx =∫ f(x) dx +∫ g(x) dx
  2. La integral del producto de una constante por una función es igual a la constante por la integral de la función.
  ∫ k f(x) dx = k ∫f(x) dx
  
  
  FUNCIÓN PRIMITIVA: 
  Una función primitiva es aquella que despues de haber sido derivada pasando por su diferencial y por el proceso de integración no vuelve exactamente a su función original
  ej:
  y=3x”+2x+18
  dy/dx=6x+2
  dy=6x+2 (dx)
  Integral=3x”+2x = 3x”+2x+c
  Integral definida: Proceso de cálculo de áreas encerrada entre una curva y un eje cartesiano.
  Función Primitiva: Relación dependiente de datos sobre uno (o más) valores, que declaran los límites de un área. Es la razón del por qué se le llama función primitiva, al ser la base del cálculo integral.
  Sean F y f dos funciones definidas sobre el mismo intervalo (o, más generalmente, dominio).
  F es una primitiva de f si y sólo si f es la derivada de F: F’ = f. 
  Mientras que la derivada de una función, cuando existe, es única, no es el caso de la primitiva, pues si F es una primitiva de f, también lo es F + k, donde k es cualquier constante real.
  Para encontrar una primitiva de una función dada, basta con descomponerla (escribirla bajo forma de una combinación lineal) en funciones elementales cuyas primitivas son conocidas o se pueden obtener leyendo al revés una tabla de derivadas, y luego aplicar la linealidad de la integral:
  Aquí están las principales funciones primitivas:
  Función F: primitiva de f función f: derivada de F
  Por ejemplo, busquemos una primitiva de x → x(2–3x). Como no se conoce primitivas de un producto, desarollemos la expresión: x(2–3x)= 2x - 3×2. 2x es la derivada de x2, 3×2 es la de x3, por lo tanto 2x - 3×2 tiene como primitiva x2 - x3 + k. Si además se pide que la primitiva verifique una condición F(x0) = y0 (que recibe el nombre de condición inicial cuando se trata de un problema de física), entonces la constante k es unívocamente determinada. En el ejemplo, si se impone F(2) = 3, entonces forzosamente k = 7. 
  
  


• ANTI DERIVADA:


• La anti derivada es la función que resulta del proceso inverso de la derivación, es decir, consiste en encontrar una función que, al ser derivada produce la función dada.


• Por ejemplo:
  Si f(x) = 3×2, entonces , F(x) = x3, es una antiderivada de Observe que no existe una derivada única para cada función. por ejemplo, si G(x) = x3+ 5, entonces es otra antiderivada de f(x).
  La antiderivada también se conoce como la primitiva o la integral indefinida se expresa de la siguiente manera: en donde: f(x) es el integrando; dx, la variable de integración o diferencial de x y C es la constante de integración.
   La anti derivada es la función que resulta del proceso inverso de la derivación, es decir, consiste en encontrar una función que, al ser derivada produce la función dada.
  Por ejemplo:
  Si f(x) = 3×2, entonces, F(x) = x3, es una antiderivada de f(x). Observe que no existe una derivada única para cada función. Por ejemplo, si G(x) = x3+ 5, entonces es otra antiderivada de f(x).
  La antiderivada también se conoce como la primitiva o la integral indefinida se expresa de la siguiente manera: en donde: f(x) es el integrando; dx, la variable de integración o diferencial de x y C es la constante de integración.
  
  Notación
  La notación que emplearemos para referirnos a una antiderivada es la siguiente:
  
  
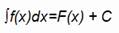  Teorema
  Si dos funciones h y g son antiderivadas de una misma función f en un conjunto D de números reales, entonces esas dos funciones h y g solo difieren en una constante.
  
  
  
  
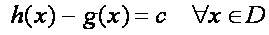
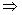  Conclusión: Si g(x) es una antiderivada de f en un conjunto D de números reales, entonces cualquier antiderivada de f es en ese conjunto D se puede escribir como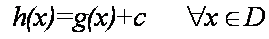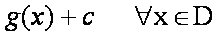c constante real.
  Fórmula que relaciona la integral definida y la indefinida
  
  
  
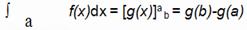
  LEYES DE LOS EXPONENTES Y RADICALES:
   LAS LEYES DE EXPONENTES SON:
  
  1. LEY DE LA MULTIPLICACION: al multiplicar dos potencias de igual base se copia la base y se suman los exponentes, para tener el exponente del producto.
     
     
  2. LEY DE LA DIVISION: al dividir dos potencias de igual base, se copia la base y al exponente del dividendo se le resta el exponente del divisor, dando el exponente del cociente.
     
     
     Estas son dos consecuencias importantes de la ley de la división:
     • PROPIEDAD DE LOS EXPONENTES NEGATIVOS: toda cantidad con un exponente negativo es un número racional, que representa el inverso multiplicativo de un número entero.
       
     • PROPIEDAD DEL EXPONENTE 0: al dividir dos cantidades exactamente iguales que tengan idéntico exponente, obtendremos una expresión con exponente cero, que también será equivalente a la unidad.
       
  3. LEY DE LA INVOLUCION, O ELEVAR A UNA POTENCIA: al elevar una potencia a un exponente, se copia la base y se multiplican los exponentes.
     
     
  4. LEY DE LA EVOLUCION, O DE LA EXTRACCION DE RAICES: al extraer la raíz de una potencia, se copia la base de la cantidad subradical, y al exponente de este subradical se le divide el índice de la raíz.
     
     
  • Esta es una consecuencia natural de la ley de extracción de raíces: una expresión radical cualquiera puede transformarse en una expresión en notación exponencial.
    
  • 
    
  • FACTORIZACION:  
  • En álgebra, la factorización es expresar un objeto o número (por ejemplo, un número compuesto, una matriz o un polinomio) como producto de otros objetos más pequeños (factores), (en el caso de números debemos utilizar los números primos) que, al multiplicarlos todos, resulta el objeto original. Por ejemplo, el número 15 se factoriza en números primos 3 × 5; y a²-b² se factoriza como binomio conjugados (a - b)(a + b).
  • La factorización de enteros en números primos se describe en el teorema fundamental de la aritmética y la factorización de polinomios (en ciertos contextos) en el teorema fundamental del álgebra
    .Factor común
    Sacar el factor común es añadir la literal común de un polinomio, binomio o trinomio, con el menor exponente y el divisor común de sus coeficientes, y para sacar esto, hay una regla muy sencilla que dice: Cuadrado del primer término más o menos cuadrado del segundo por el primero más cuadrado del segundo, y no hay que olvidar, que los dos que son positivos iguales funcionan como el primer término, sabiendo esto, será sumamente sencillo resolver los factores comunes.
    Factor común monomio
    Factor común por agrupación de términos
    

    

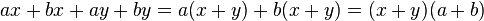    y si solo si el polinomio es 0 y el tetranomio nos da x.

    Factor común polinomio

    Primero hay que determinar el factor común de los coeficientes junto con el de las variables (la que tenga menor exponente). Se toma en cuenta aquí que el factor común no solo cuenta con un término, sino con dos. un ejemplo:

    

    Se aprecia claramente que se está repitiendo el polinomio (x-y), entonces ese será el factor común. El otro factor será simplemente lo que queda del polinomio original, es decir:
    

    

    La respuesta es:
    

    

    En algunos casos se debe utilizar el número 1, por ejemplo:
    

    

    Se puede utilizar como:
    

    

    Entonces la respuesta es:
    

    

    Caso II - Factor común por agrupación de términos

    Para trabajar un polinomio por agrupación de términos, se debe tener en cuenta que son dos características las que se repiten. Se identifica porque es un número par de términos.
    Un ejemplo numérico puede ser:
    

    

    entonces puedes agruparlos de la siguiente manera:
    

    

    Aplicamos el caso I (Factor común)
    

    

    

    Trinomio Cuadrado Perfecto

    Se identifica por tener tres términos, de los cuales dos tienen raíces cuadradas exactas, y el restante equivale al doble producto de las raíces del primero por el segundo. Para solucionar un Trinomio Cuadrado Perfecto debemos reordenar los términos dejando de primero y de tercero los términos que tengan raíz cuadrada, luego extraemos la raíz cuadrada del primer y tercer término y los escribimos en un paréntesis, separándolos por el signo que acompaña al segundo término, al cerrar el paréntesis elevamos todo el binomio al cuadrado.

    

    

    Ejemplo 1:
    

    

    Ejemplo 2:
    

    

    Ejemplo 3:
    

    

    Ejemplo 4:
    

    

    Organizando los términos tenemos
    

    

    Extrayendo la raíz cuadrada del primer y último término y agrupándolos en un paréntesis separados por el signo del segundo término y elevando al cuadrado nos queda:
    

    

    Al verificar que el doble producto del primero por el segundo término es -20xy determinamos que es correcta la solución. De no ser así, esta solución no aplicaría.
    
    LEYES DE LOGARITMOS:
     Log_b  x = y  si  y  sólo  si    b^y   =  x   donde   b, x > 0   
    

    
    

    En la expresión  log_bx  =  y,   “y “ es el logaritmo,  “x”  es el argumento del logaritmo y  “b”  la base.   A esta expresión se le llama la forma logarítmica y a la expresión 

    b^y  = x  se le llama la forma exponencial.  Compare ambas formas y note que el logaritmo de x en base b es el exponente al cual se eleva  la  b  para que de  x.

    
    

    Ejemplos:

    
    

    1.  Halle el     log₂ 8              Solución:  log₂ 8  es  el exponente al cual se eleva el 2 para que la potencia sea 8.    Por lo tanto,  log₂ 8 = 3

    
    

    2.  Halle el   log₃ 81              Solución:  log₃ 81 es  el exponente al cual se eleva el 3 para que la potencia sea  81.   Por lo tanto, log₃ 81 = 4

    
    

    Leyes de logaritmos

    
    

    1.)        log_b (MN) = log_b M + log_b N                                                                     Ejemplo:

    
    

                                                                                                  log₂ (8x16) = log₂ 8 + log₂ 16

                                                                                                       log₂ 128      =    3     +      4

                                                                                                                  7     =    7

    2.)        log_b (M/N)  =  log_b M – log_b N                                                                  Ejemplo:

                                                                                                                                                                                                   

                  log₃ (27/3)   =  log₃ 27 – log₃ 3

                                                                                                        log₃     9       =     3      –   1

                                                                                                                   2       =     2

       

    3.)        log_b Mⁿ   =   n log_b M                                                                                                            Ejemplo:

    
    

                                                                                                                                                                log₂ 32²        =  2 log₂ 32

                                                                                                                                                                log₂ 1024     =  2 ( 5  )

                                                                                                                                                                            10       =  10

    
    

    
    

    Logaritmos comunes

    
    

    Logaritmos comunes son logaritmos con base 10.  Si no se escribe la base, se sobreentiende que la misma es 10. 

    
    

    Esto es,    log  1000  =  log₁₀ 1000 = 3 

    Logaritmos naturales

    
    

    Logaritmos naturales (ln) son logaritmos con base  e=2.71828…

    Esto es,    ln  42  =  log_e  42 

    
    

    Logaritmos en otras bases

                Log_M N                                              Ejemplo:   Log₃ 56 =  = 3.664

    
    

    Tipos de problemas

    
    

    Sólo hay tres tipos de problemas de logaritmos.  Estos son:

    
    

    1)    Dados la base y el logaritmo, hallar el argumento (potencia).

                Ejemplo:   Log₃ x =  - 4                   

    Solución:  La forma exponencial equivalente a la forma dada es:   3^-4 = x

                                                                                                                       (1/3)⁴  =  x

                                                                                                                         1/81  = x           

    
    

    2)    Dado el argumento y el logaritmo, hallar la base.

    Ejemplo:   Log_x 2 = 1/5                   

    Solución:  Forma exponencial:   x^1/5  =  2

                                                               (x^1/5))⁵  =  2⁵                                                    

    
    

    3)    Dados el argumento y la base, hallar el logaritmo.

    Ejemplo:   Log₂ 7 =           = 2.8…

    
    

    LOGARITMOS:

     Productos notables es el nombre que reciben aquellas multiplicaciones con expresiones algebraicas cuyo resultado puede ser escrito por simple inspección, sin verificar la multiplicación que cumplen ciertas reglas fijas. Su aplicación simplifica y sistematiza la resolución de muchas multiplicaciones habituales.

    Cada producto notable corresponde a una fórmula de factorización. Por ejemplo, la factorización de una diferencia de cuadrados perfectos es un producto de dos binomios conjugados y recíprocamente.
    FACTOR COMÚN: El resultado de multiplicar un binomio a+b con un término c se obtiene aplicando la propiedad distributiva:
    

    

    Esta operación tiene una interpretación geométrica ilustrada en la figura. El área del rectángulo es
    

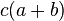    (el producto de la base por la altura), que también puede obtenerse como la suma de las dos áreas coloreadas (ca) y (cb).

    Ejemplo

    

    Binomio al cuadrado o cuadrado de un binomio

    Para elevar un binomio al cuadrado (es decir, multiplicarlo por sí mismo), se suman los cuadrados de cada término con el doble del producto de ellos. Es decir:
    

    

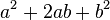    un trinomio de la forma: , se conoce como trinomio cuadrado perfecto.
    Cuando el segundo término es negativo, la ecuación que se obtiene es:
    

    

    En ambos casos el tercer término tiene siempre signo positivo.
    

    Ejemplo

    

    simplificando:
    

    

    Producto de dos binomios con un término común

    Cuando se multiplican dos binomios que tienen un término común, se suma el cuadrado del término común con el producto el término común por la suma de los otros, y al resultado se añade el producto de los términos diferentes.
    

    

    Ejemplo

    

    agrupando términos:
    

    

    luego:
    

    

    
    

    PRODUCTO NOTABLE:

     Productos notables es el nombre que reciben aquellas multiplicaciones con expresiones algebraicas cuyo resultado puede ser escrito por simple inspección, sin verificar la multiplicación que cumplen ciertas reglas fijas. Su aplicación simplifica y sistematiza la resolución de muchas multiplicaciones habituales.

    Cada producto notable corresponde a una fórmula de factorización. Por ejemplo, la factorización de una diferencia de cuadrados perfectos es un producto de dos binomios conjugados y recíprocamente.
    
    Sabemos que se llama producto al resultado de una multiplicación. También sabemos que los valores que se multiplican se llaman factores.
    Se llama productos notables a ciertas expresiones algebraicas que se encuentran frecuentemente y que es preciso saber factorizarlas a simple vista; es decir, sin necesidad de hacerlo paso por paso.
    Se les llama productos notables (también productos especiales) precisamente porque son muy utilizados en los ejercicios.
     A continuación veremos algunas expresiones algebraicas y del lado derecho de la igualdad se muestra la forma de factorizarlas (mostrada como un producto notable).
    Cuadrado de la suma de dos cantidades o binomio cuadrado
    

    a2 + 2ab + b2 = (a + b)2

    
    El cuadrado de la suma de dos cantidades es igual al cuadrado de la primera cantidad, más el doble de la primera cantidad multiplicada por la segunda, más el cuadrado de la segunda cantidad.
    Demostración:
    

    

    
    

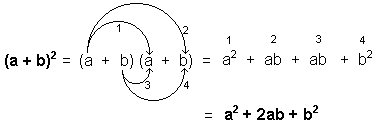    Entonces, para entender de lo que hablamos, cuando nos encontramos con una expresión de la forma a² + 2ab + b² debemos identificarla de inmediato y saber que podemos factorizarla como (a + b)²
    
    
    
    
    LIMITES:
    En matemática, el límite es un concepto que describe la tendencia de una sucesión o una función, a medida que los parámetros de esa sucesión o función se acercan a determinado valor. En cálculo (especialmente en análisis real y matemático) este concepto se utiliza para definir los conceptos fundamentales de convergencia, continuidad, derivación, integración, entre otros.
    El concepto se puede generalizar a otros espacios topológicos, como pueden ser las redes topológicas; de la misma manera, es definido y utilizado en otras ramas de la matemática, como puede ser la teoría de categorías.
    Para fórmulas, el límite se utiliza usualmente de forma abreviada mediante lim como en lim(a_n) = a o se representa mediante la flecha (→) como en a_n → a.
    
    La definición de límite matemático para el caso de una sucesión nos indica intuitivamente que los términos de la sucesión se aproximan arbitrariamente a un único número o punto L, si existe, para valores grandes de n. Esta definición es muy parecida a la definición del límite de una función cuando x tiende a .
    Formalmente, se dice que la sucesión a_n tiende hasta su límite L, o que converge o es convergente (a L), y se denota como:
    

    

    si y sólo si para todo valor real ε>0 se puede encontrar un número natural N tal que todos los términos de la sucesión, a partir de un cierto valor natural n mayor que N converjan a L cuando n crezca sin cota.
    Escrito en un lenguaje formal, y de manera compacta:
    

    

    Este límite, si existe, se puede demostrar que es único. Si los términos de la sucesión no convergen a ningún punto específico, entonces se dice que la sucesión es divergente.